Алгебра 7 клас. Лінійна фінкція, її графік та властивості.

ЛІНІЙНА ФУНКЦІЯ, ЇЇ ГРАФІК ТА ВЛАСТИВОСТІ

https://www.youtube.com/watch?v=1wJ3PoCONpo

Визначення лінійної функції

Лінійною функцією називають функцію, що задається формулою y = bx + c, де x – аргумент; с, b - константи.

Якщо зокрема, k=0, то одержуємо сталу функцію y=b;
якщо b=0, то одержуємо пряму пропорційність y=kx.

Властивості функції y=kx+b

1.Область визначення - множина всіх дійсних чисел

2. Функція y=kx+b загального виду, тобто ні парна, ні непарна.

3. При k>0 функція зростає, а при k<0 спадає на всій числовій осі.

Графіком функції є пряма.

Приклад 1.Побудувати графік функції, заданої формулою у=-1,5х+2. Користуючись графік, знайти:

а) значення у, яке відповідає х=-1;

б) значення х, якому відповідає у=-2,5.

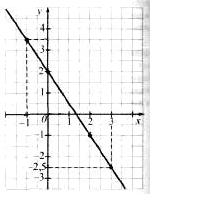
Будуємо графік функції

	y=-1,5x+2
x	0	2
y	2	-1

а) Нехай х=-1. Через точку (-1;0) проводимо пряму, паралельну осі у, і знаходимо точку її перетину з графіком. Це точка (-1; 3,5). Отже, значення х=-1 відповідає значенню у=3,5.

б) Нехай у=-2,5. Через точку (0; -2,5) проводимо пряму, паралельну осі х, і знаходимо точку перетину цієї прямої з графіком. Це точка (3; -2,5). Отже, значення у=-2,5, відповідає значенню х=3.